负反馈因其可以稳定增益、减小失真、扩展带宽、变换阻抗等功能而在电子、控制等诸多领域发挥着重大作用。小至一颗电源芯片,大至一辆汽车,都在负反馈技术的帮助下使我们的生活变得更丰富。然而,负反馈的使用也是有代价的,即可能会导致系统不稳定。
为了了解系统的稳定性情况,最直接、精确的方式就是测量系统的相位裕量(Phase Margin/ PM),我们通常会使用环路分析仪进行测试。
小编今天向大家介绍另一种方法,即通过测量过冲情况(OS)得到系统的相位裕量。
电路的二阶系统化
一些常见的反馈电路,通常都是二阶系统,我们以运放容性带载为例来讨论:
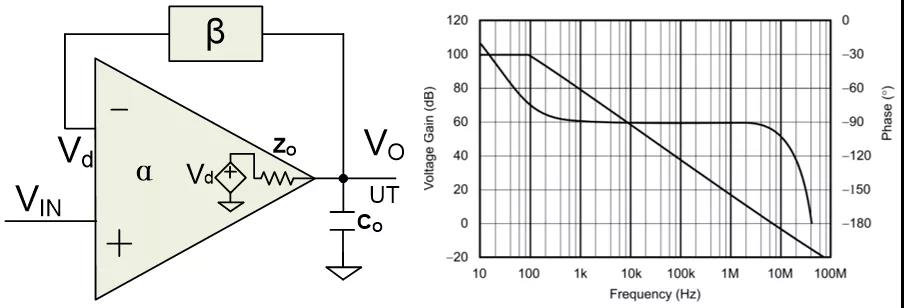
*运放的容性负载 *典型通用运放的开环增益曲线
一个典型通用运放的开环增益曲线如上图所示。它一般拥有一个低频的主极点,如100Hz,高频极点通常会被设计为远高于穿越频率,所以常规的运放电路是稳定的。
当运放存在容性负载的时候,开环输出电抗(Zo)与输出电容(Co)形成的极点会处在反馈环路内,当极点频率靠近或小于穿越频率,则会使得系统的相位裕度明显降低,导致不稳定的情况发生。
所以,一个运放带容性负载的放大电路,其传递函数可以表示为:
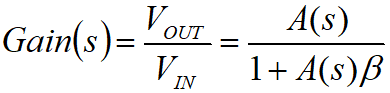
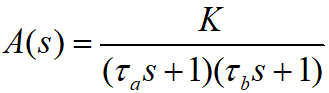
其中,K为运放的DC开环增益,β是反馈系数(作为跟随器时,β=1,100倍放大时,β=0.01)。
1/τa是运放的低频主极点的角频率,1/τb是Zo和Co产生寄生极点的角频率。可见,τa>> τb。
上式可被转换为标准的二阶系统
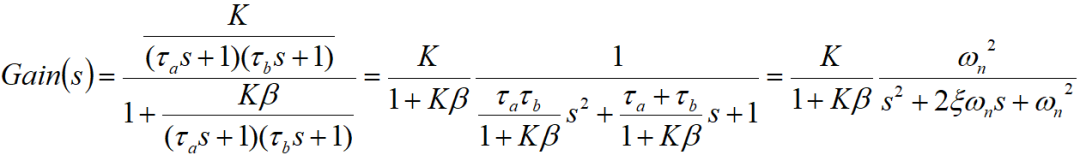
由于K为运放的DC开环增益,所以Kβ>>1
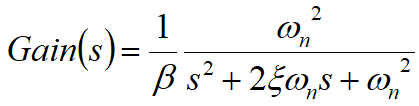
其中,ωn为电路的自然频率,ξ为阻尼系数,且
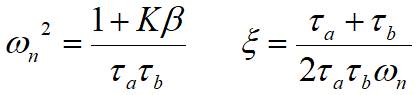
我们知道,系统处于欠阻尼状态,即0<ξ<1,才会存在过冲的情况。
对一个标准的二阶系统来说,
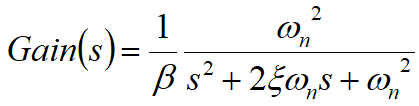
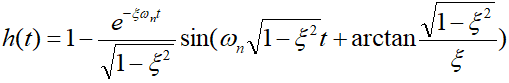
当 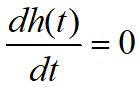
求得阶跃响应第一个峰值对应的时间为:

所以过冲为 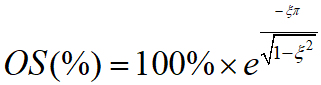
因此我们可以绘制如下过冲与阻尼系数的曲线

*过冲与阻尼系数的关系
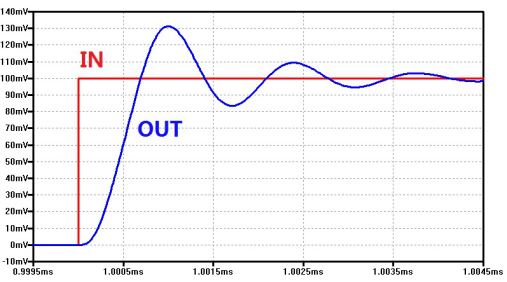
过冲可以经由在输入端给予一个小的阶跃信号,并测量输出端得到。如下图是在ξ=0.35的系统中在1ms时使用100mV阶跃输入所测得的过冲情况,过冲为31%。
相位裕量与阻尼系数的关系
我们接下去分析阻尼系数与相位裕量(Phase Margin)的关系

为了求得系统穿越频率ωc ,可令|A(s)β|=1
求得 
所以相位裕度
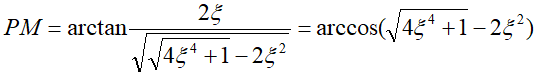
具此我们可以绘制如下相位裕量与阻尼系数的曲线

*相位裕量与阻尼系数的关系
相位裕量与过冲的关系
由此,我们借由阻尼系数,得到相位裕量与过冲的关系,绘制曲线如下
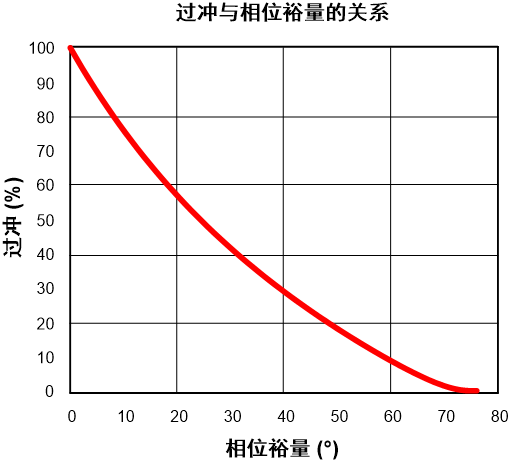
*相位裕量与过冲的关系
由上图可知,当相位裕量大于70˚以上时已经几乎没有过冲
相位裕量60˚ 时, OS(60˚)≈8.8%
相位裕量45˚ 时, OS(45˚) ≈23.4%
我们的讨论是基于二阶系统的,所以如果实际的电路并非二阶系统,那么相位裕量与过冲的关系将并不严格遵循上述推论。
但幸运的是,现实中的大部分电路都近似于二阶系统,所以通过观察过冲情况(OS)来判断系统稳定性的方法,对于有时候的系统调试(特别是,对于差分放大器或者SOC等并没有提供反馈引脚而无法采用环路分析仪的场合),或者定性分析,都是大有裨益的。